[알고리즘] 최근접 점쌍 찾기

최근접 점쌍 찾기

• 2차원 평면상에 있는 N개의 점들 중에서 서로의 거리가 가장 가까운 두 점을 찾는 문제
• 간단한 방법
  • 모든 상의 거리를 모두 계산하여 가장 가까운 쌍을 찾는 것
  • 시간 복잡도 O(N^2)
• 정렬을 사용한 방법
  • 합병 정렬 알고리즘에서 사용하는 분할-정복 기법을 사용
  • 시간 복잡도 O(N log N)
• 분할-정복 기법을 사용한 최근접 점쌍 찾기 알고리즘
  • X 좌표 값을 사용해 점을 정렬한 다음 반으로 나눔
  • 가장 가까운 쌍을 이루는 두 점은
    • 모두 한쪽 절반에 있든지 아니면
    • 하나는 한쪽 절반에, 다른 하나는 나머지 절반에 있음
  • 가장 가까운 쌍을 이루는 두 점이 분할선(dividing line)을 가로지르는 경우 효과적으로 검사할 수 있는 방법이 필요

 

알고리즘 동작 과정

동작 과정을 표로 나타 낼 수도 있습니다.

	A	B	C	D	E	F	G	H
x	5	7	3	1	9	12	10	2
y	3	11	10	6	7	5	4	2

알고리즘 시작 단계를 미리 적어놓습니다.

minValue	cp1	cp2	p1	p2	p3	p4
1000						H

표를 간단히 설명하자면, 아래와 같습니다.

minValue: p1~p4 중 두 점으로 만들 수 있는 가장 작은 거리

(만일, p1~p4로 만들 수 있는 가장 작은 거리가 없다면, 위의 값을 똑같이 적어줍니다.)

cp1, cp2: 가장 작은 거리(minValue)를 만들 수 있는 두 점

p1~p4: 해당 그룹에 있는 점

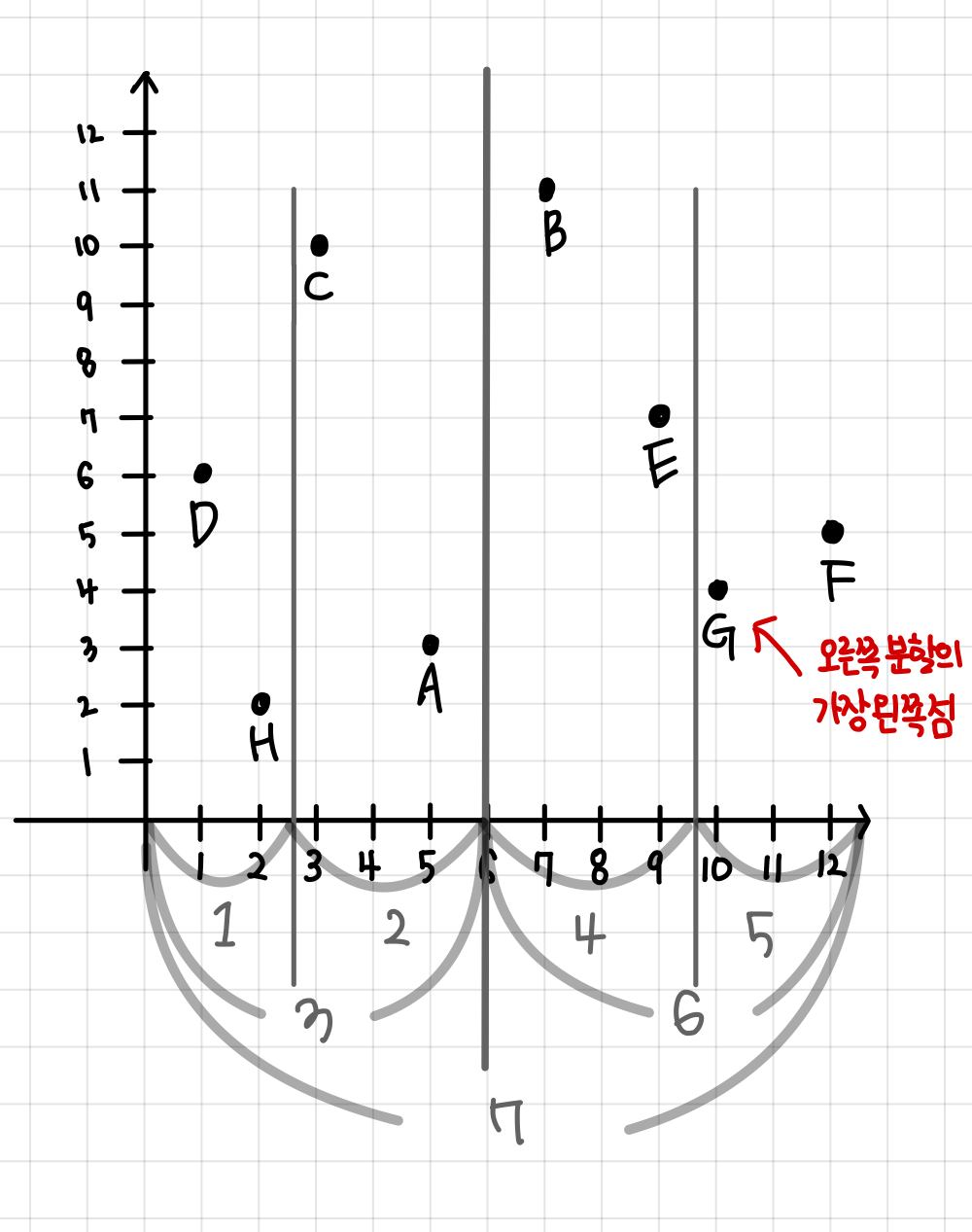
위에 점 집합들을 그림을 그려봅니다. 

 

분할 정복이므로, 보기 쉽게 구간을 나눠줍니다. 알아듣기 쉽게 N그룹이라고 호칭을 정하겠습니다.

 

주의할 점은, 합쳐지는 구간과 같이 3, 6, 7 그룹을 표에 적어줄 땐,

오른 쪽 분할 부분의 왼쪽 점P + minValue에 포함 되는 좌표만 p1~p4에 넣을 수 있습니다. 

두 점 사이의 거리 구하는 공식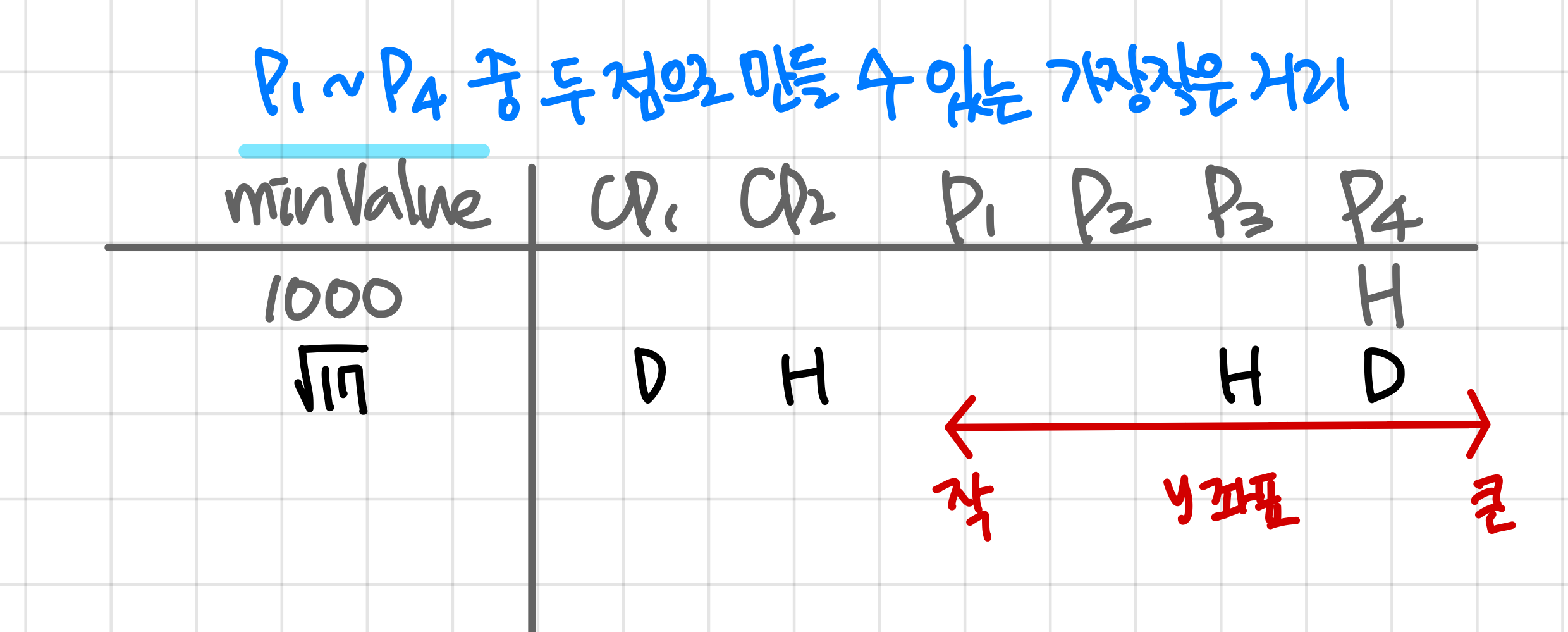

1그룹 완료 후 표

1그룹엔 H, D 가 존재 합니다.

minValue는 p1~p4에서 만들 수 있는 가장 적은 거리(HD거리)를 적어줍니다. 

위에 적혀있듯이, p1~p4는 y좌표가 작은 순서대로 적어주어야 합니다. 

 

 

2그룹 완료 후 표

2그룹엔 A, C가 존재합니다.

p1~p4에 존재하는 좌표로는 minValue를 만들 수 없기 때문에 위의 값과 동일하게 적어줍니다.

 

2그룹이 완료 된 상태입니다.

 

 

합쳐지는 3그룹은 위에서 말했듯이, 오른 쪽 분할 부분의 왼쪽 점P + minValue에 포함 되는 좌표만 넣을 수 있습니다.

minValue = √17 = 4.XX 이므로 3그룹 내에서 4칸까지 포함되는 좌표만 넣을 수 있습니다.

 

따라서, 3그룹은 H, A, D, C 좌표를 넣어 줄 수 있습니다. 

H, A, D, C를 차례대로 넣어준 다음, DH거리보다 AH거리가 더 짧기 때문에 변경해줍니다.

 

3그룹이 완료 된 상태입니다.

4그룹엔 E, B 좌표가 존재하며, BE거리 > AH거리 이기 때문에 AH로 minValue를 채워줍니다.

 

4그룹이 완료 된 상태입니다.

5그룹엔 G, F좌표가 존재하며, AH거리 > FG거리 이기 때문에 FG로 minValue를 채워줍니다.

 

5그룹이 완료 된 상태입니다.

합쳐지는 6그룹은 위에서 말했듯이, 오른 쪽 분할 부분의 왼쪽 점P + minValue에 포함 되는 좌표만 넣을 수 있습니다.

√5 = 2.XX 이므로 6그룹 내에서 2칸까지 포함되는 좌표만 넣을 수 있습니다.

따라서, 6그룹은 G, F, E 좌표를 넣어 줄 수 있습니다. 

6그룹엔 G, F, E좌표가 존재하며, FG거리보다 작은 거리는 없기 때문에 위와 동일하게 FG로 minValue를 채워줍니다.

6그룹이 완료 된 상태입니다.

 

합쳐지는 7그룹은 위에서 말했듯이, 오른 쪽 분할 부분의 왼쪽 점P + minValue에 포함 되는 좌표만 넣을 수 있습니다.

minValue = √5 = 2.XX 이므로 7그룹 내에서 2칸까지 포함되는 좌표만 넣을 수 있습니다.

따라서, 7그룹은 A, E, B 좌표를 넣어 줄 수 있습니다. 

7그룹엔 A, E, B좌표가 존재하며, FG거리보다 작은 거리는 없기 때문에 위와 동일하게 FG로 minValue를 채워줍니다.

7그룹이 완료 된 상태입니다.

 

 

 

틀린 점이 있거나, 궁금한 점이 있다면 댓글 남겨주세요

감사합니다!

 

 

 

 

 

[두 점 사이의 거리 사진]
출처:  https://m.blog.naver.com/galaxyenergy/221263626715