-
[알고리즘] 기하 알고리즘 - 2차원 트리Computer Science/Algorithm 2021. 12. 14. 04:14
2차원 트리
- 이진 트리 형태를 가지며, 동적으로 변화하는 트리
- 범위 탐색에 편리하게 사용할 수 있도록 기하학적 공간을 나눔
- 만드는 과정
- 이진 탐색 트리를 만드는 과정과 유사
- 이진 탐색트리와 다른 점은 이진 트리의 레벨에 따라 y축과 x축을 번갈아 가면서, 한번은 y좌표값을 기준으로 삽입하고, 한번은 x좌표값을 기준으로 삽입하는 것임
2차원 트리 만드는 과정
1. 해당 위치가 x좌표 or y좌표인지 확인
2. 해당 위치에 맞는 좌표와 새로 삽입할 좌표와 비교
3. 위치 선정
4. x좌표 or y좌표자리인지 확인
5. 새로운 좌표를 알맞은 좌표모양으로 그려죽;

삽입 시, x 좌표 모양 y 좌표 모양 한번은 y좌표값을 기준으로 삽입하고, 한번은 x좌표값을 기준으로 삽입해야하므로,
삽입 시 쉽게 판별할 수 있도록 다른 모양으로 그려줍니다.

삽입 과정을 상세히 보여드리겠습니다.

y좌표부터 넣어준다. y축과 x축을 번갈아가며 넣어야하므로 먼저 y좌표 부터 넣어줍니다.

이번엔 x좌표를 넣어줄 차례이므로 위치 선정 후 B좌표의 x좌표를 그려준다.

C 삽입 과정 
D 삽입 과정 
E 삽입 과정 
F 삽입 과정 
G 삽입 과정 
H 삽입 과정 
I 삽입 과정 
J 삽입 과정 
K 삽입 과정 
L 삽입 과정 
M 삽입 과정 
N 삽입 과정 
O 삽입 과정 
P 삽입 과정
2차원 트리에서 영역 (7, 10) 과 (11, 16) 에 대해 범위 탐색하는 과정에서 방문하는 노드를 표시하기
좌표 범위를
x: 7~11
y: 10~16 로 정리 할 수 있다.

방문 노드가 y=6 이므로 탐색 범위(y: 10~16)에 들어가지 않는다.
따라서, 더 큰 값으로 이동하기 위해 오른쪽 아래 노드로 방문한다.
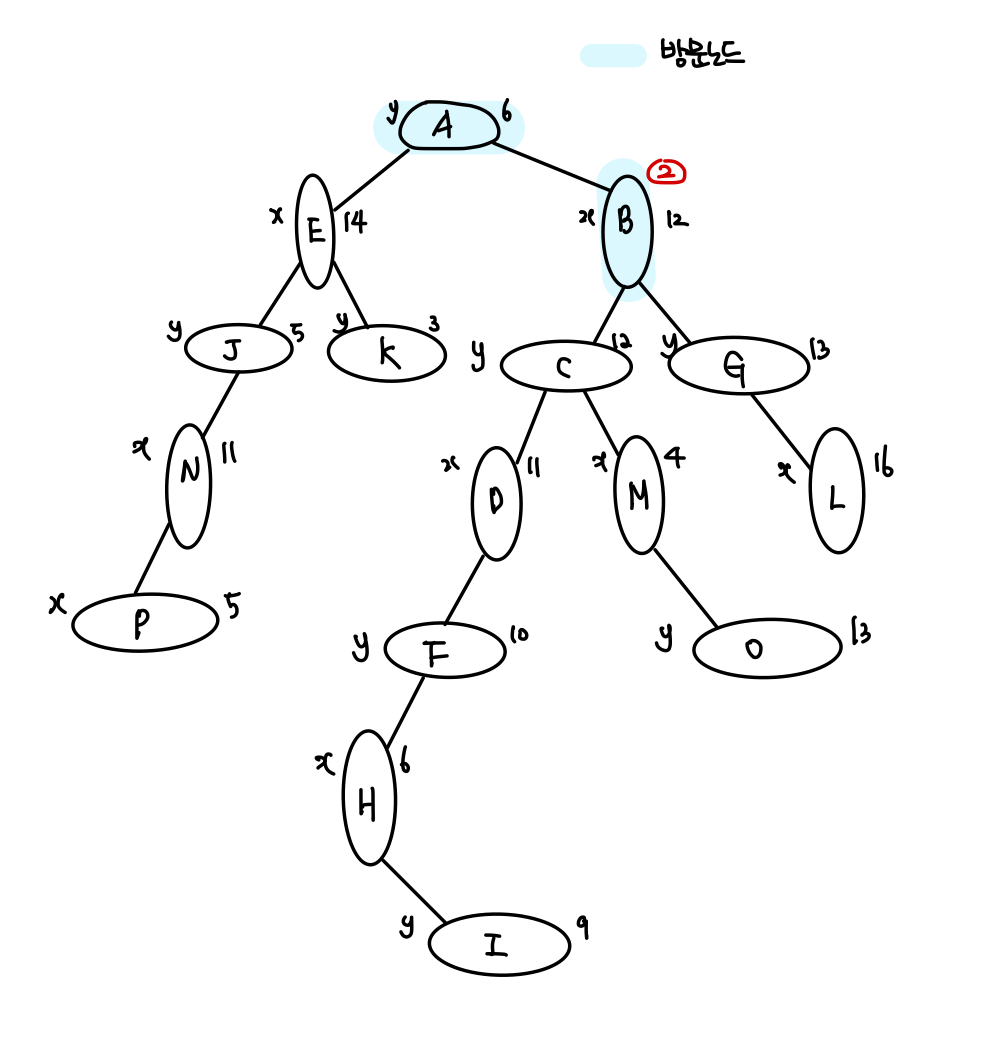
방문 노드가 x=12 이므로 탐색 범위(x: 7~11)에 들어가지 않는다.
따라서, 더 작은 값으로 이동하기 위해 왼쪽 아래 노드로 방문한다.

방문 노드가 y=12 이므로 탐색 범위(y: 10~16)에 들어간다.
따라서, 왼쪽, 오른쪽 아래 노드로 둘다 방문 할 수 있다.
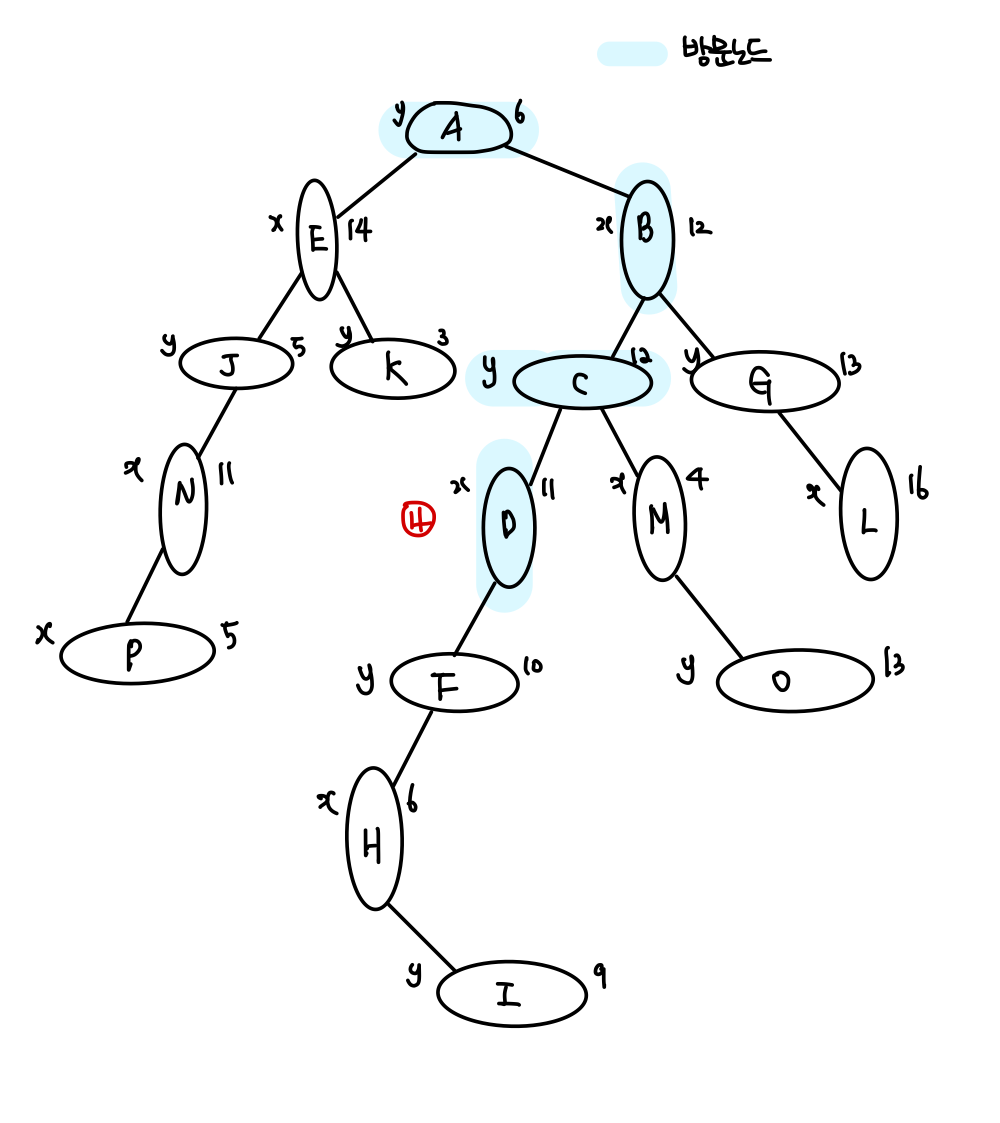
방문 노드가 x=11 이므로 탐색 범위(x: 7~11)의 최대값이다.
따라서, 왼쪽 아래 노드를 방문한다.

방문 노드가 y=10 이므로 탐색 범위(y: 10~16)의 최소값이다.
따라서, 왼쪽 아래는 탐색 범위에 벗어나고, 오른쪽 아래는 존재하지 않으므로 탐색을 멈춘다.

y=12 일 때, 둘 다 방문 할 수 있다고 했으므로, 이번엔 오른쪽 아래 노드로 방문한다.
방문 노드가 x=4 이므로 탐색 범위(x: 7~11)에 들어가지 않는다.
따라서, 더 작은 값으로 이동하기 위해 왼쪽 아래 노드로 방문해야 하는데, 존재하지 않으므로 탐색을 종료한다.

최종 방문노드 표시 'Computer Science > Algorithm' 카테고리의 다른 글
[알고리즘] 최근접 점쌍 찾기 (0) 2021.12.16 [알고리즘] 그라함 스캔 알고리즘 (0) 2021.12.15 [알고리즘] 최적 이진 탐색 트리 (0) 2021.12.14 [알고리즘] 스트링 편집 거리 (0) 2021.12.14 [알고리즘] AVL 트리 (0) 2021.10.24